.
Dies ist das Kapitel 2 (aus einer Serie von 9 Kapiteln)
Kapitel 2 beschreibt die "Grundlagen der naturgetreuen Wiedergabe" - Zur Erklärung der Hifi-Technik und der Quellen und Geräte soll dieser vorbereitende Artikel über die Physik dienen.
2.1 Elementares
Was ist Schall?
- Abb. 2.1-1 Entstehung des Schalls (Stimmgabel- schwingungen, Longitudinal- und Transversalwellen)
Sowohl bei der Aufnahme als auch bei der Wiedergabe von Rundfunksendungen, Schallplatten und Tonbanddarbietungen dient der Schall als Träger aller Informationen. Schall entsteht, wenn elastische Körper (z.B. eine Stimmgabel) in Schwingungen versetzt werden und dabei das umgebende Medium, beispielsweise Luft, zu gleichartigen Schwingungen anregen (Abb. 2.1-1). Es treten dann im Rhythmus der Schwingungen in der Luft Druckschwankungen auf, die sich als Schallwellen kugelförmig ausbreiten.
Die Schallgeschwindigkeit
Die Schallgeschwindigkeit hängt vom Medium ab, in dem sich die Schallquelle befindet. Sie beträgt in Luft bei 20°C etwa 342m/s, in Wasser (Echolot) etwa 1500m/s und in Stahl etwa 5000m/s. In Gasen und in Flüssigkeiten breitet sich der Schall in Longitudinalwellen (Längswellen) aus, während er sich in festen Körpern sowohl in Longitudinal- als auch in Transversalwellen (Querwelten) fortpflanzt.
Wellenlänge, Frequenz
Die Abb. 2.1-1 läßt noch erkennen, daß der Abstand vom Anfang bis Ende einer Sinusschwingung mit Wellenlänge (X) bezeichnet ist. Die Anzahl der Schwingungen in einer Sekunde ergibt die Frequenz (Einheit Hertz, abgek. Hz). Bei unserer Stimmgabel, die auf den sogenannten Normstimmton von 440 Hz (Kammerton a) abgestimmt ist, wird dann eine Schwingung in der Zeit von 1/440 s zurückgelegt. Mit der Schallgeschwindigkeit c = 342m/s erhält man jetzt folgende Beziehung:
Wellenlänge des Stimmgabeltones
Die Wellenlänge des Stimmgabeltones von 440 Hz beträgt somit:
.
- Abb. 2.1-2 Entstehung eines Klanges
Der von einer Stimmgabel oder von einem „Sinusgenerator" erzeugte sinusförmige reine Ton kommt in der Musik praktisch nicht vor. Bei den von Musikinstrumenten ausgehenden Schallereignissen haben wir es nicht mit reinen Tönen, sondern vielmehr mit Klängen zu tun.
.
Der Klang
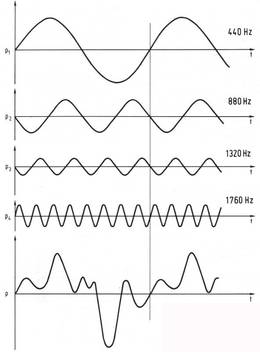
Ein Klang, entsprechend der periodisch verlaufenden Schwingung p nach Abb. 2.1-2 ist ein Hörschall, der aus einem Grundton px (z.B. 440 Hz) und drei Teiltönen besteht, deren Frequenzen ganzzahlige Vielfache der Grundfrequenz sind
(p2 = 2 • 440 Hz = 880 Hz, p3 = 3 • 440 Hz = 1320 Hz, p4 = 4 • 440 Hz = 1760 Hz).
Vorgenannte Teiltöne werden Obertöne (und weil sie Teil eines Klanges sind, auch Partialtöne) genannt. In der Schwingungslehre spricht man von Oberwellen; die erste Oberwelle einer Grundschwingung von 440 Hz ist dann ausgewiesen durch 880 Hz. Spricht man von Harmonischen, so bilden 440 Hz die erste und 880 Hz die zweite Harmonische. Mit Hilfe der Fourieranalyse (J.B. Fourier, franz. Mathematiker 1786-1830) läßt sich ein solcher komplexer Klang in eine Summe reiner Töne zerlegen.
.
- Abb. 2.1-3 Linearspektren a) einer Flöte (d2 = 570 Hz)
Die Referenz ist der Grundton
Die Musiklehre „benotet" nur den Grundton eines Instrumentes oder einer menschlichen Stimme; sie setzt für einen bestimmten Grundton, ob von einer Posaune oder einer Violinsaite, die gleiche Note, obwohl es sich hier um verschiedene „Klänge" mit zwar demselben Grundton, aber einer unterschiedlichen Anzahl von Obertönen verschiedener Stärken handelt.
.
- Abb. 2.1-3 Linearspektren b) einer Trompete (c1 = 256 Hz)
Die Obertöne
Der Klang von weich tönenden Instrumenten, beispielsweise einer Flöte oder Klarinette enthält wenig Obertöne, während der von härter oder strahlender klingenden Instrumenten, wie z.B. einer Trommel oder einer Trompete, viele Obertöne aufweist.
Der Frequenzumfang von Musikinstrumenten
Die verschiedenen Obertöne eines Klanges lassen sich in einem sogenannten Linienspektrum anschaulich darstellen (Abb. 2.1-3). Man erhält es in einem Diagramm, auf dessen "Abzisse" ?? die Frequenzen des Tonbereiches und auf der "Ordinate" ?? die Druckamplituden der einzelnen Obertöne aufgezeichnet sind.
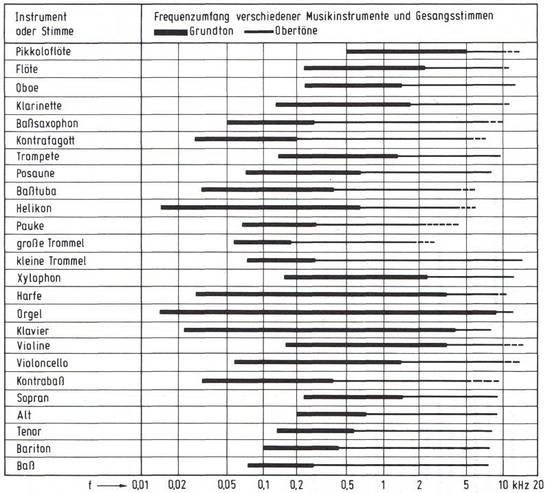
Abb. 2.1-4 zeigt den Frequenzumfang verschiedener Musikinstrumente und Gesangsstimmen, wobei zur besseren Übersicht die Oktaven vom Subkontra bis zum sechsgestrichenen c mit angegeben sind. Die dicken Striche kennzeichnen die Grundtonbereiche, die dünn ausgezogenen Striche den Obertonanteil.
- Abb. 2.1-4 Frequenzumfang verschiedener Musikinstrumente und Gesangsstimmen
- nach Oktaven sortiert
Das Ohr als Schallempfänger
- Abb. 2.1-5 a) Äußeres-, Mittel- und Innenohr
- Abb. 2.1-5 b) Längsschnitt durch die Schnecke (ausgerollt gezeichnet)
Das Ohr bildet das paarig am Kopf außen und innen angeordnete Gehörorgan, das im Innenohr Sitz des Gleichgewichtsorgans (Labyrinth) ist (Abb. 2.1-5a). Das äußere Ohr besteht aus der Ohrmuschel und dem durch den Schläfenknochen verlaufenden äußeren Gehörgang, der gegen das Mittelohr, der sogenannten Paukenhöhle, vom Trommelfell getrennt ist. In den Gehörgang gelangende Schallwellen versetzen das Trommelfell in verhältnisgleiche Schwingungen, die von den Gehörknöchelchen, bestehend aus Hammer, Amboß und Steigbügel, auf das elastische ovale Fenster der Gehörschnecke übertragen werden.
Die Schnecke
Die Schnecke (in Abb. 2.1-5b gestreckt dargestellt) ist flüssigkeitsgefüllt und wird durch eine Zwischenwand, der Basilarmembran, unterteilt. Die Pumpbewegungen des Steigbügels lassen die Flüssigkeit im Schneckengang hin- und herpendeln, wobei Wander wellen entstehen, die sich entlang der Basilarmembran ausbreiten und diese in Schwingungen versetzen.
.
- Abb. 2.1-5 c) Querschnitt durch eine Schneckenwindung
Die Basilarmembran ist auf ihrer ganzen Länge mit hochempfindlichen Sinneszellen, dem sogenannten Cortischen Organ (Abb. 2.1-5c) besetzt.
Gerät die Basilarmembran in Schwingungen, so entstehen in den Zellen elektrochemische Reize, die über die Gehörnerven in das Hörzentrum des Gehirns gelangen und dort entsprechende Höreindrücke vermitteln.
Der Vergleich zweier "Sinne"
- Abb. 2.1-6 Unterschied zwischen dem
- Sicht- und Hörfeld des Menschen
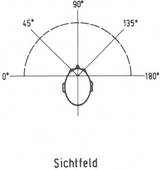
Der hochempfindliche Hörsinn bildet die wichtigste Informationsquelle des Menschen, die ihm auch unbewußt ein deutliches Bild seiner Umwelt vermittelt. So läßt sich beispielsweise im Vergleich mit dem Sichtfeld die Bedeutung des Gehörs anschaulich darstellen (Abb. 11-6). Während das Sichtfeld des Menschen nur etwa 180° beträgt, ermöglicht das Hörfeld zu allen Tageszeiten eine Runduminformation von 360°.
Der Hörbereich
Überschreiten die Schalldruckschwankungen die sogenannte Hörschwelle (Abb. 2.1-7), so vermögen sie das Trommelfell zu gleichen Schwingungen anzuregen. Wie man aus dem Verlauf der Hörschwelle ersieht, hängt die Hörbarkeit des Schalls nicht nur von seiner Intensität, sondern auch von der Frequenz ab. Bei mittleren Frequenzen (zwischen 1000 und 4000 Hz) ist die Hörempfindlichkeit am größten, so beträgt beispielsweise der Schalldruck bei 1.000Hz 0,00002 Pa = 2 • 10"5 Pa = 20 uPa.
- Abb. 2.1-7 Hörfläche des menschlichen Ohres von der Hörschwelle bis zur Schmerzgrenze
Stark unterschiedliche Empfindlichkeit
Zu tieferen und zu höheren Frequenzen hin nimmt die Empfindlichkeit sehr stark ab. Das Ohr kann beispielsweise einen Ton von 40 Hz erst dann wahrnehmen, wenn der Schalldruck etwa lOOOmal größer ist als der eines 1000Hz Tones. Mit steigendem Schalldruck vermindert sich die Frequenzabhängigkeit des Gehörs, und die Kurve verläuft annähernd geradlinig, wenn der Schalldruck die „Schmerzgrenze" mit ca. 10 2 Pa erreicht.
(Als Schalldruck bezeichnet man den durch die Schallschwingungen hervorgerufenen Wechsel druck je Flächeneinheit, der bisher in ubar, neuerdings in Pascal (Pa) angegeben wird. 1 Pa= 10ubar= 1 N/m2).
Der Schalldruck
- Abb. 2.1-8 Unterschied zwischen Schalldruck und Schalldruckpegel
Der auf das Gehör wirkende Schalldruck ändert sich bei 1000 Hz zwischen der Hörschwelle p0 = 0,00002 Pa = 2 • 10'5 Pa und der Schmerz grenze ps = 100 Pa = 102 Pa im Verhältnis 1:10 Millionen.
Um diesen großen Bereich überschaubar zu machen, hat man einen logarithmischen Maßstab mit der Einheit Dezibel (dB) gewählt. Aus dem erwähnten linearen Schalldruckverhältnis p0 : ps = 1:10 000 000 = 1 : 107 ergibt sich dann ein Schall(druck)pegel-Verhältnis in dB von
20-log-=20-log 107 = 20- 7= 140 dB. Ps
Solche Berechnungen führt man am besten an Hand einer dB-Tabelle aus (siehe Seite 199, Tab. 10-1)
Das "Phon"
Die Einheit der Lautstärke wird mit „Phon" bezeichnet. Als Lautstärkeskala gilt die auf 1 kHz bezogene logarithmische Skala des Schallpegels zwischen der Hörschwelle und der Schmerzgrenze (siehe Mittelachse in Abb. 2.1-7).
Den Unterschied zwischen Schalldruck in Pa und Schalldruckpegel in dB veranschaulicht die Abb. 2.1-8.
Die Lautheit
Unter Lautheit versteht man die Stärke der Schallempfindung. Sie soll der Stärke der Schallwahrnehmung proportional sein und wird in „sone" angegeben. Da die unmittelbare Bestimmung der Lautheit sehr schwierig ist, hat man die Definition an den Lautstärkepegel geknüpft (DIN 45630).
Die zugrunde gelegte Beziehung beruht auf der Erfahrung, daß eine Änderung des Lautstärkepegels um 10dB eine Verdoppelung bzw. Halbierung der "Wahrnehmungsstärke" bewirkt. 40 phon entsprechen 1 sone, 50 phon = 2 sone und 60 phon = 4 sone usw.
Das Richtungshören
- Abb. 2.1-9 Laufzeitunterschied bei seitlich eintreffendem Schall zwischen zu- und abgewandtem Ohr des menschlichen Kopfes
Mit seinen beiden Ohren kann sich der Mensch in seiner Umgebung auch akustisch orientieren. Die Fähigkeit, die Richtung zu bestimmen, aus der das Schallsignal kommt, beruht darauf, daß das Schallsignal unsere Ohren in unterschiedlicher Zeit und Intensität erreicht.
Wie aus Abb. 2.1-9 zu ersehen, gelangt das seitlich auffallende Schallsignal an das rechte Ohr eher (früher) als an das linke. Hier muß es noch den Weg (Wegdifferenz 1) um den Kopf herum zurücklegen. Die Laufzeit ist daher größer als bis zum rechten Ohr.
Es geht um Millisekunden
Der Laufzeitunterschied ändert sich mit dem Einfallswinkel (gamma) und macht sich schon bei 1°, d.h. bei Zeitspannen im Bereich von Millisekunden (ms) bemerkbar. Bei 90°, wenn der Schall von der Seite kommt, ist er am größten. Bei seitlich eintreffendem Schall werden auch Intensitätsunterschiede in den Ohren verursacht, weil der Kopf das gegenüberliegende Ohr schallmäßig abschattet.
2.2 Stereo-Wiedergabe
- Abb. 2.2-1 Prinzip der Monoübertragung
Bis Ende der 50er Jahre erfolgten elektro-akustische Übertragungen nur einkanalig (Abb. 2.2-1). Bei dieser „monofonen" Übermittlung ist es dem Hörer nicht möglich, einzelne Instrumente im Klangkörper zu lokalisieren, weil bei der Wiedergabe über einen Lautsprecher die Intensität und die „Phasenlage" der Schallschwingungen auf beide Ohren stets gleich bleiben.
Der Vorteil von 2 Kanälen
- Abb. 2.2-2 Prinzip der Stereoübertragung
Um die Wiedergabe zu verbessern, d.h. der Originaldarbietung soweit wie möglich anzugleichen, versuchte man vor allem die der monofonen Übermittlung fehlende räumliche Ausdehnung der komplexen Schallquellen zu erreichen. Das Problem glaubte man dadurch lösen zu können, daß man im Aufnahmeraum eine große Anzahl Mikrofone aufstellte und über entsprechend viele Kanäle ebensoviele Lautsprecher im Wiedergaberaum betrieb. Hierbei stellte sich jedoch überraschender Weise heraus, daß allein zwei Kanäle die besten Ergebnisse brachten (Abb. 2.2-2).
Die Summenlokalisation
Dies läßt sich durch die Summenlokalisation der Intensitäts- und Laufzeit-unterschiede zweier nebeneinander arbeitender Lautsprecher erklären. Als Summenlokalisation wird die Fähigkeit des menschlichen Gehörs bezeichnet, die von zwei Lautsprechern ankommenden Signale zu einem resultierenden Schalleindruck umzubilden, wobei man davon ausgeht, daß die Lautsprecher in einem gewissen Abstand voneinander (Basis) aufgestellt sind und der Hörer sich auf der Symmetrielinie vor den beiden Lautsprechern befindet (Abb. 2.2-3).
Summenlokalisation durch Intensitätsunterschiede
Strahlen beide Lautsprecher die gleichen Signale, z.B. die Ansage eines Sprechers, mit gleicher Lautstärke ohne zeitliche Verzögerung ab, so hat der Hörer den Eindruck, daß sich der Sprecher in der Mitte zwischen den Lautsprechern befindet. Die Richtung, in der der Hörer den Sprecher vermutet, wandert jedoch aus der Symmetrielinie heraus auf jenen Lautsprecher zu, dessen Intensität sich gegenüber dem anderen vergrößert. Dieser „Lokalisationseffekt" tritt nur bei Frequenzen oberhalb 800 Hz auf.
- Abb. 2.2-3 Summenlokalisation durch Intensitäts- und Laufzeitunterschiede. Lokalisation der vom Hörer empfundenen Schallquelle gegen die Symmetrielinie zweier Lautsprecher durch Intensitätsunterschiede. Lokalisation der vom Hörer empfundenen fiktiven Schallquelle gegen die Symmetrielinie zweier Lautsprecher durch Laufzeitunterschiede der Schallsignale.
Summenlokalisation durch Laufzeitunterschiede
Treffen bei gleicher Lautstärke die Signale der beiden Lautsprecher gegeneinander verzögert beim Hörer ein (Abb. 2.2-3), so ist ebenfalls eine Ortung der scheinbaren Schallquelle möglich, und zwar bei Frequenzen zwischen 300 und 800 Hz. Strahlen beide Lautsprecher dasselbe Signal mit gleicher Lautstärke, jedoch einer von ihnen mit zeitlicher Verzögerung (r) gegenüber dem anderen ab, so verschiebt sich der Ort, an dem die scheinbare Schallquelle empfunden wird, auf den Lautsprecher zu, dessen Signal unverzögert beim Hörer eintrifft. Dieses akustische Phänomen wird als „Gesetz der ersten Wellenfront" bezeichnet.
Der (uns allen inzwischen bekannte) Zusammenhang zwischen der Hifi-Qualität und der Stereophonie steht detailliert im Kapitel 2.3 samt der Hifi-Norm.
.
