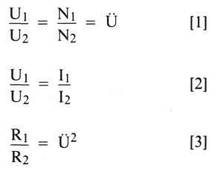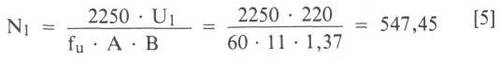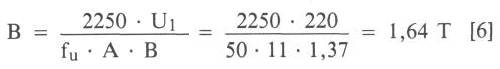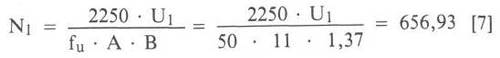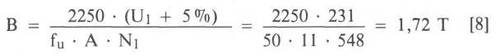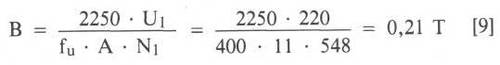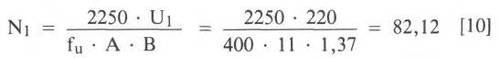Ein ELRAD Artikel aus 1978 Heft 6 Teil 1 von 2
von Gert Redlich im Jan. 2021 - Eine PDF-Version dieses Artikels wurde uns im Jan 2021 zugesandt. Der Artikel erschien in der "elrad" im Juni Heft 1976 mit einer Menge Formeln und Bildern und Zeichnungen. Das Thema ist von Gerhard Haas sehr anschaulich und verständlich dargestellt. Teil 2 kommt auf der nächsten Seite.
.
Der Übertrager - das unbekannte Wesen - 1987 Teil 1
elrad 1987, Heft 6 - von Gerhard Haas
Weil Röhrenverstärker seit einiger Zeit ein Come- back erleben, sind Übertrager wieder in das Bewußtsein gerückt. Zum Teil wird aus ihnen ein Mythos gemacht.
Obwohl von vielen Hifi-Enthusiasten in ihren Anlagen verpönt, hat der Übertrager gerade in diesem Bereich nach wie vor große Bedeutung. Daß er aber auch ein normales elektronisches Bauteil ist, wie man mit ihm umgeht, ihn im NF-Bereich richtig einsetzt und seine enge Verwandtschaft zum Netztrafo, das soll diese Artikelserie aufzeigen.
Im ersten Abschnitt wird die zum Verständnis notwendige Theorie erarbeitet. Im zweiten Abschnitt werden einige typische Anwendungen erklärt und was dabei jeweils besonders zu beachten ist. Im dritten Abschnitt wird zu guter Letzt ein Ausgangsübertrager für eine Röhrenendstufe exemplarisch durchgerechnet (worauf wir hier im Museum aber verzichten wollen.).
Das Wissen aus Theorie und Praxis
Bevor wir in die Theorie einsteigen, seien einige Betrachtungen vorangestellt. Der halbleiter- und chipverwöhnte Elektroniker nimmt den Übertrager in erster Linie nur noch als lästig schweres Bauteil in Form des Netztrafos zur Kenntnis, das ihm die Niederspannungen galvanisch getrennt vom Netz für seine Chips liefert.
Dabei tut er ihm Unrecht, denn Trafos und Spulen sind mit die ältesten elektronischen Bauteile überhaupt. Ohne sie wäre vieles nicht möglich. Selbst in modernsten Meßgeraten und Computern findet man sie, allerdings oft in solcher Form, daß sie nur Kennern sofort auffallen.
Die Erfindung oder besser die Entdeckung, daß ein stromdurchflossener Leiter ein Magnetfeld erzeugt, was Grundvoraussetzung für Übertrager ist, wurde schon 1820 durch den Physiker Hans Christian Oersted (1777-1851) gemacht.
Ihm zu Ehren wurde bis zur Umstellung auf das SI-System die Einheit Oe (= Oersted) für die magnetische Feldstärke (A/m) benutzt. Weitere Forschungen führten dann zur Drahtspule, zur Spule mit Eisenkern und letztendlich zu Übertragern.
Zum Vergleich: Der erste Transistor wurde erst 128 Jahre später erfunden. Bis die ersten brauchbaren ICs erhältlich waren, vergingen nochmals rund 20 Jahre. An dieser Stelle sei gleich vorweg die Bemerkung angebracht: Netztrafos werden in dieser Artikelserie aufgrund vieler gleichartiger Eigenschaften und Konstruktionsprinzipien Ausgangsübertragern gleichgestellt, da sie im Prinzip ja nichts anderes sind, als ein auf eine bestimmte Frequenz (50 Hz, 60 Hz bzw. 400 Hz in der Flugzeugtechnik) optimierter Transformator.
Bei den alten Röhrenverstärkern unverzichtbar
In uralten Röhrenverstärkern waren sehr oft zwischen jeder Stufe Trenn- und Anpaßübertrager geschaltet. Die preiswerte Massenproduktion von Kondensatoren und Widerständen war damals noch nicht in diesem Umfang möglich, so daß das bekannte und erforschte Bauteil Übertrager oft leichter beherrschbar war.
Wer Schaltpläne von Rundfunkgeräten und Verstärkern aus der Vorkriegszeit studiert, wird feststellen, daß sehr viele Spulen und Übertrager darin enthalten sind, vergleichsweise aber wenig Kondensatoren und Widerstände.
Als zum Anfang der Halbleiterära nur PNP-Transistoren erhältlich waren, fand man Übertrager in den Treiber- und Ausgangsstufen der Lautsprecherverstärker. Damit waren die notwendige Phasenumkehr und die gewünschte Leistung mit AB-Endstufen am einfachsten zu bewerkstelligen. Wer genaue Vergleiche anstellt, wird feststellen, daß die ersten Transistorverstärker im Prinzip nichts anderes als modifizierte Röhrenverstärker waren.
Seit Anfang der siebziger Jahre verschwanden dann praktisch alle Übertrager aus den elektronischen Geräten, denn mit den Halbleiterchips ging es ja einfacher, leichter, besser, billiger.
Stückzahlen im Millionen-Bereich
Den meisten Elektronikern ist wahrscheinlich gar nicht bewußt, wo und in welchen Stückzahlen Übertrager heute eingesetzt werden. Damit man nur eine ungefähre Ahnung bekommt, wo überall Übertrager im weitesten Sinne eingesetzt werden, seien nur einige der wichtigsten Bereiche genannt:
.
In Telefonen der Gabelübertrager, in Modems. Antennen-Anpaßübertrager in Antennen, in Rundfunk- und Fernsehempfängern sowie Videorecordern, in der Medizintechnik zur galvanischen Trennung von Mensch und Maschine, zur galvanischen Trennung in Meßgeräten, in der Studiotechnik in Tonbandmaschinen und Mischpulten, in Rundfunkanstalten, Anpaßübertrager für Moving Coil Systeme, in Schaltnetzteilen, in der 100V-Technik in ELA-Anlagen und vieles mehr.
Wenn man sich klarmacht, daß wenige Windungen Kupferlackdraht um einen Ferritkern gewickelt im Hochfrequenzbereich auch zum Oberbegriff Übertrager gehören - ebenso wie ein großer Ausgangsübertrager für einen Röhrenverstärker (denn es gelten prinzipiell dieselben Berechnungs- und Konstruktionsbedingungen), kann man sich die täglich produzierten und im Betrieb befindlichen Stückzahlen vorstellen - sie gehen in die Millionen!
.
Über das Ziel dieser beiden Artikel - "Entmythologisieren"
Obwohl Übertrager in sehr großen Stückzahlen produziert werden, ist es in der Literatur relativ ruhig um sie geworden. Was an Grundlagenwissen vor allem im NF-Bereich zu vermitteln war, wurde bereits in den zwanziger bis fünfziger Jahren ausgiebig abgehandelt, so daß es eine Reihe von zum Teil sehr guten Veröffentlichungen schon lange nicht mehr zu kaufen gibt.
Was kluge Leute vor Jahrzehnten in umfangreichen Spezialwerken in Theorie und Praxis abgehandelt haben, kann diese Artikelreihe nicht ersetzen. Am Ende soll jedoch das Thema NF-Übertrager entmythologisiert und der normale Elektroniker in der Lage sein, einen NF-Übertrager richtig zu behandeln und in einer Schaltung einzusetzen.
Der Übertrager - ein vermeintlich sehr einfaches Bauteil
Im Prinzip ist ein Übertrager ein sehr einfaches Bauteil. Man nimmt Kupferlackdraht, wickelt ihn in zwei galvanisch getrennten Wicklungen auf einen Spulenkörper, steckt einen passenden Eisenkern hindurch (oder auch nicht), und fertig ist der Übertrager.
Leider steckt der Teufel im Detail. Es gibt eine Vielzahl von Möglichkeiten, den Draht zu wickeln. Dann gibt es viele verschiedene Isolationsmaterialien und sehr viele verschiedene Trafokerne. Je nachdem, was wie kombiniert wird, entsteht einmal ein hochwertiger Übertrager, das andere Mal ein Drahthaufen mit oder ohne Eisenkern.
Übertrager bieten sich immer dann an, wenn eines der drei Grundelemente des Ohmschen Gesetzes nicht paßt. Dies sagen die drei Grundformeln aus:
.
Die Theorie und die Realität
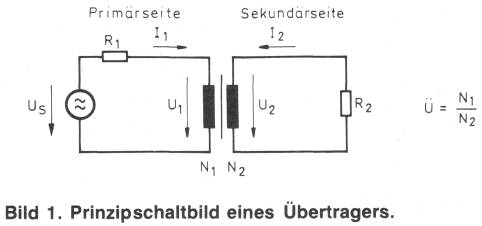
In Bild 1 sind nochmals die Formelzeichen und die Verhältnisse am Übertrager eingezeichnet. Wie aus den Formeln 1 bis 3 ersichtlich, ist der Übertrager ein ideales Bauteil, da sich mit ihm sehr elegant unpassende Verhältnisse von Strom, Spannung und Widerstand den Bedürfnissen anpassen lassen. Der Übertrager wäre also ideal, wenn er nicht real wäre.
Nach Bild 1 würde der ideale Übertrager die Spannung U1 in die Spannung U2 bei vollständiger galvanischer Trennung übersetzen. Ebenfalls würden die Ströme und die Widerstände nach den Formeln 2 und 3 entsprechend übersetzt werden.
In der Realität sieht es aber so aus, daß sowohl auf der Primär- als auch auf der Sekundärseite eine Reihe von Faktoren zu berücksichtigen sind, die das ideale Bauteil Übertrager auf den Boden der Realitäten zurückbringen. Bevor wir diese Faktoren untersuchen. zählen wir sie kurz auf.
.
In der Realität muß man also folgende Faktoren berücksichtigen
Diese sind die Kupferwiderstände (Gleichstromwiderstand) der Wicklungen, die Wicklungskapazitäten sowie die durch die Beschallungen entstehenden Kapazitäten, die Wicklungsinduktivität, die Streuinduktivität und das Verhalten des Eisenkerns sowie dessen Verluste.
Was hier in wenigen Worten gesagt wurde, ist im Grunde genommen ein sehr komplexes Gebiet, das sich nicht kurz abhandeln läßt. Wollte man alles halbwegs erschöpfend behandeln, wäre ein Buch fällig.
Bauen wir uns ein theoretisches Modell ....
Wie bei allen elektronischen Bauteilen mit komplexem Verhalten kann auch für den Übertrager ein Modell herangezogen werden, das alle wichtigen Faktoren berücksichtigt, wenn die Rahmenbedingungen genauer definiert werden.
Der Übertrager nach Bild 1 wäre ideal und für alle Frequenzen gleichermaßen geeignet. Wie aber bereits erwähnt, sind im realen Übertrager frequenzabhängige Faktoren vorhanden (Induktivität und Kapazitäten), die entsprechend berücksichtigt werden müssen.
.
Wir betrachten hier nur den NF (Audio-) Bereich
Das Gebiet, das vorzugsweise in dieser Artikelserie untersucht werden soll, beschränkt sich auf den NF-Bereich von 20 Hz ... 20 kHz sowie auf Übertrager mit Eisenkern.
Damit sind schon die ersten Voraussetzungen für ein brauchbares Grundmodell geschaffen, das uns den Ansatz zu einer genaueren Untersuchung gibt.
.
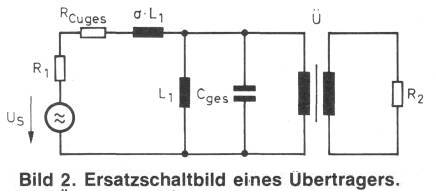
- Bild 2. Ersatzschaltbild eines Übertragers.
.
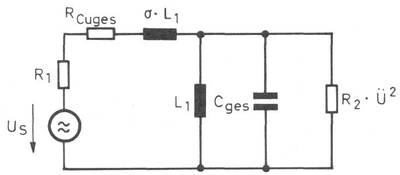
In Bild 2 ist der reale Übertrager mit allen Komponenten dargestellt, die im NF-Bereich zu berücksichtigen sind, wobei schon alle das Übertragungsverhalten beeinflussende Größen auf die Primärseite transformiert sind. Zum besseren Verständnis muß diese Maßnahme erklärt werden.
Mit "ü" stellt man sich einen idealen Übertrager vor. Damit werden alle auf der Sekundärseite auftretenden Schaltungsteile auf die Primärseite mit dem Faktor "ü" übersetzt und können dort zusammengefaßt werden. Dies erleichtert die Betrachtung und Berechnung erheblich. R2 kann ebenfalls auf die Primärseite transformiert werden, woraus dann das Ersatzschaltbild nach Bild 3 entsteht.
.
Zum Verständnis müssen wird das Ersatzschaltbild vereinfachen
Damit man das ganze Gebilde in den Griff bekommt, muß man untersuchen, welche Komponenten bei welchen Frequenzen wirksam sind. Um die ganze Sache weiter zu vereinfachen, können wir die Kupferwiderstände bis auf weiteres vernachlässigen, weil man davon ausgehen kann, daß bei einem gut konstruierten Übertrager die Kupferwiderstande mindestens fünfmal kleiner sind als die Abschlußwiderstande.
.
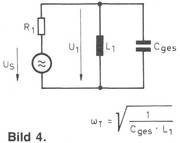
Bild 4 zeigt nun das vereinfachte Ersatzschaltbild für tiefe Frequenzen,
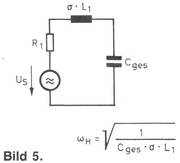
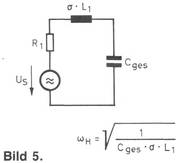
Bild 5 das für hohe Frequenzen mit den dazugehörigen Formeln.
Bei tiefen Frequenzen ist der Betrag der Streuinduktivität so klein, daß ihr Einfluß vernachlässigt werden kann. Bei hohen Frequenzen kann die Primärinduktivität unberücksichtigt bleiben, da sie praktisch einen unendlich großen Widerstand darstellt.
.
Die Bedeutung der Resonanzstellen
Nach den Formeln in den Bildern 4 und 5 gibt es zwei Resonanzstellen. Nach dem Schaltbild in Bild 4 ergibt sich ein Parallelresonanzkreis. Bei Parallelresonanz wird die Impedanz des Schwingkreises sehr groß, theoretisch unendlich.
Diese Resonanzstelle tritt jedoch in der Frequenzgangkurve lediglich als geringe Welligkeit hervor, da dieser Schwingkreis durch die dann auftretenden Verluste im Übertrager sowie durch den in der Regel sehr niedrigen Innenwiderstand des Signalgenerators stark bedämpft wird.
Die zweite Resonanzstelle tritt weit mehr in Erscheinung und verdient deshalb besondere Beachtung. Sie wird im wesentlichen vom Wert [??L1] bestimmt. Der Wechselstromwiderstand des Übertragers wird bei dieser Resonanzstelle aufgrund des Serienresonanzkreises Null.
Dadurch wird der Strom in diesem theoretisch unendlich. Die Resonanzspitze tritt im Frequenzgang deutlich in Erscheinung und wird nur durch den Innenwiderstand des Signalgenerators sowie die Übertragerverluste und den sekundären Abschlußwiderstand bedämpft.
R1 ist aber relativ klein, und bei Spannungsanpassung ist R2 relativ groß (siehe auch Bild 3), so daß die Dämpfung überwiegend den Übertragerverlusten zufällt. Ist R1 sehr klein, wird die Sekundärspannung an der Resonanzstelle sehr viel größer, als es vom Übersetzungsverhältnis her zu erwarten ist. Darüber fällt die Frequenzgangkurve steil ab.
Ganz wichtig - die untere Grenzfrequenz
Die untere Grenzfrequenz des Übertragers muß auch besonders beachtet werden. Die gesamten Kapazitäten sind an der unteren Frequenzgrenze zu vernachlässigen, da "Cges" praktisch als unendlich großer Widerstand angesehen werden kann. Deshalb gilt bei den unteren Frequenzen die Formel Us = I1 (Rl + jwL1).
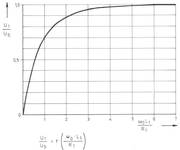
Wie sich der Übertrager bei sehr tiefen Frequenzen verhält, läßt sich am einfachsten feststellen, wenn Us und U1 sowie R1 und coL1 ins Verhältnis gesetzt werden.
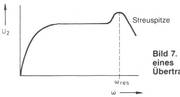
Dies ist in Bild 6 mit der dazugehörigen Formel dargestellt. In Bild 7 ist die Frequenzgangkurve für die Sekundärspannung dargestellt, wobei alle bisherigen Erkenntnisse darin verwertet sind.
.
Die Streuspitze und der Frequenzgang eines Übertragers .....
Nachdem wir nun den typischen Frequenzgang eines Übertragers kennen und wissen, wie er zustande kommt, können wir jetzt schon eine Aussage machen. Man hört und liest immer wieder davon, daß z.B. ein Mischpult oder ein Verstärker, in dem ein Übertrager eingesetzt ist, entweder einen guten oder auch schlechten Klang hat. Klangverfälschend wirkt sich vor allem die Streuspitze aus, wenn sie nicht weit genug über 20 kHz liegt. Bei guter Line- und Mikrofonübertragern liegt diese Spitze bei 100 kHz und sollte so klein wie möglich sein.
Wenn man z.B. 1:1 (sogenannte) Line-Übertrager nachmißt, kann man je nach Hersteller und Typ Resonanzspitzen mit Überhöhung zwischen 2 dB und bis über 20 dB feststellen. Die Resonanzstelle in der Mitte des Übertragungsbereiches muß möglichst klein sein, damit der Frequenzgang glatt bleibt. Die Welligkeit muß unter ±1dB je nach Übertrager und Einsatzfall sein. Größere Welligkeiten wirken sich wie fest eingestellte Klangregler aus. Wird im Mittenbereich zu stark angehoben, klingt das Gerät blechig und unausgewogen.
Was ein Übertrager insgesamt unter Berücksichtigung der Streuspitze (die über 100 kHz liegen soll) können muß, kann dem IRT-Pflichtenheft entnommen werden (IRT = Institut für Rundfunktechnik). In der Regel sind Studioverstarker immer irgendwo (Eingang/Ausgang) mit einem Übertrager bestückt. Ein Pflichtenheft-Verstärker muß folgenden Frequenzgang haben:
60 Hz ... 10 kHz ±0,5 dB
40 Hz ... 15 kHz ±0,5/-2dB.
Damit liegt auch die untere Bereichsgrenze fest. 40 Hz muß ein Trafo einwandfrei übertragen; darunter darf der Klirrfaktor ansteigen. Das Ohr ist außerdem in diesem Bereich relativ unempfindlich gegenüber höheren Klirrfaktorwerten.
.
Jetzt geht es zur "Transformatoren-Hauptgleichung"
Eine weitere sehr wichtige Formel ist die sogenannte Transformatoren- Hauptgleichung.
.
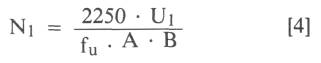
- Formel-04
.
- N1 = Primärwindungszahl
- U1 = Primärspannung in V
- fu = untere Grenzfrequenz in Hz
- A = Eisenquerschnitt in cm²
- B = Induktion in T
.
Neue Maßeinheiten - aus "Gauß" wird "Tesla"
Sie steht in vielen alteren Lehrbüchern noch in etwas anderer Form, die wir hier aber nicht mehr bringen wollen. Die angegebene Formel ist auf die neuen Einheiten nach dem Sl-System bezogen, wobei die einschneidendste Änderung die Umstellung des Maßes der Induktion von Gauß auf Tesla ist.
(Hier nochmals zur Erinnerung: 10.000 Gauß = 1 Tesla, abgekürzt T.)
Diese Trafo-Hauptformel dient zur Ermittlung der Primärwindungszahl, wobei maximale Induktion B, Primärspannung U1, untere Grenzfrequenz fu und der Eisenquerschnitt A gegeben sein müssen.
Um die Formel verständlich zu machen, rechnen wir exemplarisch einen Modelltrafo durch, der eine untere Grenzfrequenz von 60 Hz noch einwandfrei übertragen soll.
Weiterhin setzen wir einen Kern nach DIN 41 302 der Größe M 102 A mit der Blechqualität V 230-50 A voraus mit einer maximal zulässigen Induktion von 1,37 T und einem Eisenquerschnitt von 11cm2. Damit ist dieses Blechpaket laut Tabelle für 143 VA Sekundärleistung geeignet. Nehmen wir noch als Spannung die Netzspannung von 220 V, so ergibt sich folgende Rechnung:
Halbe Windungen gibt es normalerweise nicht, deshalb sind für diesen Trafo 548 Primärwindungen notwendig.
Jetzt wollen wir untersuchen, was passiert, wenn dieser Trafo bei gleicher Primärspannung mit 50 Hz betrieben wird. Dazu stellen wir die Trafohauptgleichung nach B um und erhalten
Wenn man von 60 Hz auf 50 Hz "umsteigt"
Wie man sieht, ist die Induktion jetzt 1,64 T, also 20% höher als bei 60 Hz. Die Folge wäre, daß der Eisenkern in die Sättigung kommt, weil für ihn nur 1,37 T zugelassen sind. Man kann sich den Effekt der Sättigung auch so vorstellen:
In einem bestimmten Eisenkern ist eine endliche Menge magnetisierbarer Teilchen vorhanden, die Menge ist durch die maximal mögliche Induktion B beschrieben. Versucht man nun den Kern weiter zu magnetisieren, ist dies unmöglich, da sich alle magnetischen Teilchen schon ausgerichtet haben. Die weitere Folge ist, daß der Trafo das Signal erheblich verzerrt, heiß wird und stark streut.
Die Amerikaner wundern sich immer, warum ihre Trafos in Hamburg heißer werden als in New York!
.
Man kann 60 Hz Trafos bei uns nicht einfach so betreiben
Dem aufmerksamen Leser wird bereits aufgefallen sein, daß mit den eben gemachten Modellrechnungen bereits zwei Fliegen mit einer Klappe geschlagen wurden.
Erstens muß bei der Berechnung mit der Trafohauptgleichung bei gegebenem Kern die untere Grenzfrequenz berücksichtigt werden, die verzerrungsfrei übertragen werden soll.
Zweitens wurde bewiesen, warum ein auf amerikanische Verhältnisse (60Hz-Netz) optimierter Trato nicht einfach durch Umschalten von 110 V auf 220 V an dem europäischen 50Hz-Netz betrieben werden kann. Eine Reihe amerikanischer Audio-Import-Geräte selbst aus dem Profi-Studiobereich fällt beim Betrieb in Deutschland durch heiße Trafos und Brummeinstreuungen auf.
Auf Rückfrage beim amerikanischen Hersteller hin bekommt man als Antwort, daß diese Probleme dort nicht bekannt sind. Was für ein Wunder!
Die untere Grenzfrequenz ist ein Maßstab
Wenn man vor dem Problem steht, eine tiefere untere Grenzfrequenz verarbeiten zu müssen, bieten sich mehrere Lösungen an. Die Primärspannung U1 kann verkleinert werden. denn bei kleinerer Eingangsspannung (also bei kleinerer übertragener Leistung) wird der Trafo nicht so weit in die Sättigung gesteuert.
Um es wieder auf die Modellrechnung zu beziehen: Statt 220 V dürfen auf der Primärseite nur noch 183,5 V anliegen, was am Stromnetz wohl kaum möglich ist. Bei einem Übertrager in einem Röhrenverstärker kann die Primärspannung zurückgenommen werden, indem man die Aussteuerung reduziert. Dann läßt sich die noch sauber übertragbare untere Grenzfrequenz absenken, bis die Primärinduktivität ihre Wirkung zeigt (siehe Bild 6).
Wenn eine tiefere untere Grenzfrequenz bei gleichbleibend hoher Leistung übertragen werden soll, bleibt nur noch die Möglichkeit, einen umkonstruierten Trafo zu nehmen.
.
Eine Lösung : den Trafo "umkonstruieren"
Die einfachste Möglichkeit wäre, bei gleichem Kern die Primärwindungszahl zu erhöhen. Um wieder auf das Modell zurückzugreifen:
Beim 50Hz-Betrieb ergeben sich nach der Hauptformel
Windungen hoch gerundet, also 657 Windungen, notwendig (= 20% mehr).
Bei Übertragern, die z.B. 40 Hz bis 25 kHz verarbeiten müssen, ist diese Windungszahl- Erhöhung nicht immer problemlos durchführbar. Doch davon später.
Bei gleicher Windungszahl und Primärspannung bleiben also nur noch eine höhere Induktion und ein größerer Eisenquerschnitt übrig, wenn von 60 Hz auf 50 Hz übergegangen werden soll.
Höhere Induktion erreicht man dadurch, daß man eine bessere Blechsorte auswählt. Wie wir bereits berechnet haben, tritt eine maximale Induktion von 1.64 T unter den gegebenen Verhältnissen auf. Exakt diesen Wert erreicht man z.B. mit besseren, "kornorientierten" M-Blechen (VM 111-35), die statt 0,5mm Stärke wie beim Ausgangsblech (mit nur 1,37 T Belastbarkeit) auch nur 0,35mm stark sind.
.
Eine anderen Kern auswählen
Eine weitere Möglichkeit wäre, auf den noch besseren Kern MD 102 A überzugehen, der bei praktisch gleichem Eisenquerschnitt sogar mit 1,72 T belastbar ist. Es bliebe eine Reserve von rund 5%, die durchaus ihre Berechtigung hat, wie wir gleich sehen werden. (Was es mit den verschiedenen Kerntypen und Materialien auf sich hat, wird später noch ausführlich behandelt.)
Universelle Netz-Trafos grundsätzlich für 50 Hz berechnen
Ist der Trafo auf 50Hz und 220V optimal berechnet, treten keine Probleme auf. Aber auch das beste Netz hat Schwankungen, ±6% ist ein durchaus gängiger Wert, den die E-Werke angeben und garantieren.
Rechnen wir wieder an unserem Modelltrafo nach, was passiert, wenn die Netzspannung sich um 5% erhöht.
Der Kern MD 102 A würde also bei 5%iger Netzüberspannung gerade noch nicht in die Sättigung kommen - wie man sieht, eine notwendige Reserve ! Bei Netzunterspannung gibt es diesbezüglich keine Probleme.
.
Der Trick für Flugzeuge - das 400 Hz Bordnetz
Ziehen wir nun der Vollständigkeit halber die Rechnung unseres Trafos mit der üblichen Frequenz von 400 Hz für Bordnetze von Flugzeugen durch. Dann ergibt sich unter den gegebenen Bedingungen eine Maximalinduktion von
Die Induktion ist bei achtmal höherer Frequenz nur ein Achtel. Zäumen wir das Pferd noch einmal anders herum auf, indem wir zuerst die nötige Windungszahl für 400 Hz ermitteln und die maximale Induktion von 1,37 T ausnutzen.
Nun noch die Berechnung der möglichen Primärspannung unter Ausnutzung der maximalen Induktion bei 548 Windungen.
Wenn also unser Modelltrafo entsprechend isoliert ist, kann eine bis zu 6.67mal höhere Primärspannung eingespeist werden, bevor der Kern in die Sättigung kommt ! Leistungsmäßig kann dieser Kern unter diesen Bedingungen rund 44,5mal mehr Leistung übertragen.
.
Damit ist auch erklärt, warum Flugzeug-Bordnetze mit höherer Frequenz (400Hz) arbeiten. Bei einer bestimmten Trafogröße ist mit 400Hz mehr Leistung übertragbar bzw. eine bestimmte Leistung mit einem viel kleineren Kern (was erhebliche Gewichtseinsparung und Volumenverkleinerung bedeutet!).
.
Übertrager (oder Trafos) in Schaltnetzteilen
Schaltnetzteile profitieren ebenfalls von dieser Gesetzmäßigkeit.
Hier können beispielsweise Trafos mit nur 10x10x6cm Baugröße und einer Arbeitsfrequenz von etwas über 20 kHz gut 2000 W übertragen.
Für dieselbe Leistung wäre bei 50 Hz ein EI 231 B erforderlich, der rund 23x23x23cm groß ist und voll bewickelt gut 30kg auf die Waage bringt.
Rechts ein Beispiel - der BOSE 1800 Kraftverstärker
.
Zurück zum Thema - NF-Leistungsübertrager
Um diese Feststellungen auf den NF-Leistungsübertrager anzuwenden: Der Übertrager muß leistungsmäßig auf die untere Grenzfrequenz optimiert werden, höhere Frequenzen bereiten bis zu gewissen Grenzen keine Probleme.
Inzwischen haben wir schon eine ganze Reihe von Kenntnissen über den Übertrager (Trafo) angesammelt und die wichtigen Punkte aufgezeigt.
Wenn einem die Trafohauptgleichung sowie die Einflüsse der Primärinduktivität und der Streuinduktivität einigermaßen geläufig sind, könnte man annehmen, in der Lage zu sein, einen Übertrager zu berechnen und zu bauen. Leider genügt das bisherige Wissen bei weitem nicht.
Wer sich von einem Trafoblechhersteller die Datentabellen näher angesehen hat, wird unter anderem auch die Angaben Windungen pro Volt auf der Primärseite, Windungen pro Volt auf der Sekundärseite und den Wirkungsgrad finden. Wie alles auf dieser Welt ist auch ein Trafo nicht verlustfrei, was sich in den Zahlenangaben widerspiegelt.
Wer also einen Übertrager mit einer Spannungsübersetzung von exakt 1:1 herstellen möchte, kann dies nicht dadurch erreichen, daß er primär- und sekundärseitig lediglich die gleiche Windungszahl aufbringt. Vor allem wenn Leistung übertragen werden soll (und dies gilt bei kleinen Übertragern auch schon im Milliwattbereich), müssen die Verhältnisse der Windungszahlen entsprechend angepaßt werden.
.
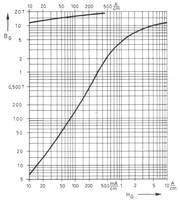
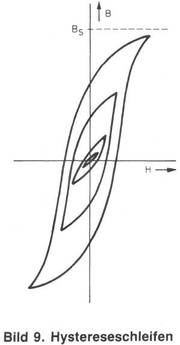
Die Magnetisierungskurven für Trafobleche
In Bild 8 ist eine typische Magnetisierungskurve für Trafoblech dargestellt, in Bild 9 sind die für Trafos mit Eisenkern typischen Hysteresekurven bei verschiedener Aussteuerung aufgezeigt. Anschaulich kann man sich die Trafoverluste im Kern und die daraus resultierenden Kurven folgendermaßen vorstellen:
Die magnetisierbaren Teilchen des Eisenkerns befinden sich im Ruhezusland. Um sie in ihrer Lage zu verändern, muß Energie eingesetzt werden - wobei sich die am leichtesten drehbaren Teilchen zuerst nach den Feldlinien ausrichten. Je mehr Teilchen ausgerichtet sind, desto schwieriger wird es, die restlichen auch noch dazu zu bringen. Dies äußert sich in der Verflachung der Kennlinie.
Wer es noch anschaulicher braucht, nimmt einen Magneten und hält ihn unter ein Stück Pappe, auf dem Eisenfeilspäne liegen. Ein Teil der Spane wird sich bereits ausrichten, wenn der Magnet angenähert wird. Viele werden sich nach den Feldlinien des Magneten ausrichten, wenn man an die Pappe klopft (Energiezufuhr), und ein hartnäckiger Rest richtet sich kaum oder gar nicht nach den Feldlinien aus.
Wo die Verluste bei Trafos herkommen
Weil dies so ist, muß in den Übertrager primärseitig mehr Leistung eingespeist werden, als er sekundärseitig abgibt. Dazu kommt, daß für bestimmte Kerntypen bestimmte Spulenkörper vorgesehen sind. Dies bedingt, daß nur eine gewisse Menge Kupfer untergebracht werden kann. Damit sind überwiegend auch die Kupferverluste festgelegt. Je nach Blechqualität und Kerngröße ergeben sich deshalb Wirkungsgrade zwischen etwa 40% und 98%.
Ein Trafo mit nur 60% Wirkungsgrad heizt sich ordentlich auf. Da solch schlechte Wirkungsgrade aber nur bei relativ kleinen Kernen 'erreicht' werden, sind sie nicht die großen Energieverschwender. Wenn sehr hochwertige, kornorientierte Bleche bei gutem, streuarmem Blechschnitt, wie z.B. dem MD-Schnitt, verwendet werden, ist bereits ab Kerngröße MD 55 ein Wirkungsgrad von 77% erreichbar, bei MD 102 B sind es immerhin 93,5%.
Zum Vergleich: auch modernste Automotoren und die Arbeitspferde des Transports, die großen Dieselmotoren, haben einen maximalen Wirkungsgrad von nur 25 ... 30%.
Es gibt aber noch mehr wichtige Details
Nachdem nun einige grundsätzliche, die Übertragereigenschaften bestimmende Dinge untersucht sind, müssen wir uns der Betrachtung wichtiger Details zuwenden.
Wie wir bereits gesehen haben, hängt der glatte Frequenzgang von mehreren Faktoren ab. Die untere Grenzfrequenz wird im wesentlichen von L1 bestimmt. L1 hängt ab vom verwendeten Kern und der Windungszahl (maximal zulässige Induktion, geforderte Mindestinduktivität).
Wie bereits demonstriert, kann im Zweifelsfall die Primärwindungszahl erhöht werden, damit L1 und Bmax die richtigen Werte bekommen. Daß dies aber nicht unbedingt der einzig richtige Weg sein muß, soll im folgenden aufgezeigt werden.
.
Weitere Alternativen zum Verlust-Ausgleich
Dazu müssen wir die Faktoren Übersetzungsverhältnis und Wicklungskapazität sowie die Streuinduktivität genauer untersuchen. In Bild 10a und b sind die wirksamen Kapazitäten zwischen den einzelnen Lagen und Drähten dargestellt.
Bild 10a zeigt eine Lagenwicklung mit Zwischenisolation, in Bild 10b ist eine Lagenwicklung auf Lücke gewickelt (in der keine Lagenisolation möglich ist).
Man kann die Wicklungskapazität theoretisch exakt berechnen. Jedoch führt diese Berechnung auch nicht wesentlich weiter als eine Näherungsformel, und mit dieser kommt man auch nur weiter, wenn man nicht nur genau die Dielektrizitätskonstanten der verwendeten Drähte, Isolationen und, bei Tränkung des Wickels, die des Lacks kennt. Dann muß auch noch geprüft werden, inwieweit der Lack tatsächlich in die Wicklung eingebracht wird.
Nahezu vollständige Durchdringung erreicht man nur mit dünnflüssigen, heißen Lacken im Vakuumofen. Für hochwertige Übertrager ist eine Wickeltechnik nach Bild 10a besser, da in etwa nur die halbe Lagenkapazität wie nach Bild 10b entsteht.
Außerdem können Lagenisolationen untergebracht werden, die gegebenenfalls die Lagenkapazität weiter vermindern, was sich positiv auf die Streuspitze im Frequenzgang auswirkt (siehe Bild 5 und 7), indem sie sich verkleinert.
.
Die Streuinduktivität
Ein sehr wichtiges Kriterium für einen Übertrager ist die "Streuinduktivität". Wenn man in der Literatur nach Berechnungsformeln dafür sucht, so findet man den lapidaren Satz, 'eine genaue Berechnung der Streuinduktivität eines Transformators ist nicht möglich'.
Damit sind wir mit unserer Weisheit genauso weit wie bei der Berechnung der Wicklungs- kapazität. Wie aus dem Ersatzschaltbild des Übertragers für hohe Frequenzen (Bild 5) hervorgeht, ist in der Formel der Faktor [deltaL1] enthalten.
Dieses delta kann eventuell mit Näherungsformeln berechnet werden, man kann aber genausogut 2%, 5%, 7% oder einen ähnlichen Wert einsetzen. Bei der Berechnung eines Übertragers nutzt dies aber sehr wenig, weil sich die Wicklungskapazitäten und Schaltkapazitäten, die ja in der Formel in Cges enthalten sind, auch nur in etwa abschätzen lassen.
.
Der Begriff der Kopplung
Wickelkapazitäten und Streuinduktivität bekommt man trotz aller eben aufgezeigten Schwierigkeiten in den Griff, wenn man dazu einige praktische Überlegungen anstellt. Dazu müssen wir noch den Begriff der Kopplung einführen.
In der Regel will man für gute NF-Übertrager eine feste Kopplung, denn es soll ja auf der Sekundärseite möglichst das herauskommen, was man in die Primärseite hineinschickt. Was der Übertrager an Leistung in der Wicklung selbst verbraucht, was im nutzlosen Streufeld verlorengeht oder was an Ummagnetisierungsverlusten in den Blechen in Wärme umgesetzt wird, trägt nichts zur Leistungsübertragung bei. Streuverluste und Wicklungskapazitäten kann man nicht einzeln betrachten, eines spielt in das andere hinein.
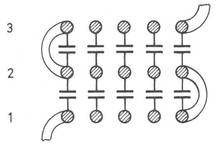
Die Streuung hängt ebenso wie die Wicklungskapazität vom Aufbau des Wickels ab. Hier können wir ein gutes Stück am Übertragergeheimnis entmythologisieren, denn jetzt kommen wir auf die Verschachtelung zu sprechen. Wie jeder Elektroniker weiß, wird beim Parallelschalten von Kondensatoren die Gesamtkapazität größer, bei Reihenschaltung wird sie kleiner, und zwar kleiner als die kleinste eingesetzte Kapazität der Reihenschaltung.
Beim kapazitätsarmen Wicklungsaufbau eines Übertragers tut man nichts anderes. Dabei schlägt man gleich zwei Fliegen mit einer Klappe. Wenn Primär- und Sekundärwicklung ineinander verschachtelt werden, sinkt durch die automatisch entstehende Reihenschaltung der Einzelkapazitäten die gesamte Wicklungskapazität. Außerdem wird der Kopplungsgrad erhöht, was wiederum die Streuinduktivität senkt.
.
Die Verschachtelung der verschiedenen Übertrager
Ob ein Übertrager nun letztendlich 6fach, 9fach oder 12fach verschachtelt ist, tut nichts zur Sache. Ein 12fach verschachtelter Übertrager kann durchaus schlechter sein als ein 6fach verschachtelter.
Bei falsch gewählter Wicklungsunterteilung, gekoppelt mit einer Lagenisolation, die durch ihre hohe Dielektrizitätskonstante die Kapazität erhöht statt erniedrigt, trägt nichts zur Qualitätssteigerung bei. Lediglich die Bewicklung wird teurer.
Bei Röhrenendstufen muß eine Mindestmenge an Isolation in den Wickel gepackt werden, und er sollte vakuumgetränkt werden, damit die geforderte Spannungsfestigkeit erreicht wird. Dies darf jedoch nicht auf Kosten des Kopplungsfaktors gehen.
Zu dicke Isolationen vermindern den Kopplungsfaktor und erhöhen die Streuinduktivität, so daß dünnere Isolation und Vakuumtränkung der bessere Weg sind.
Die Wirkung von Windungen und Lagen
Wie man sieht, kann mit richtiger oder falscher Wickeltechnik viel gut oder schlecht gemacht werden. Zudem widersprechen sich eine Reihe von Forderungen (Isolation z.B. ist notwendig und nicht vermeidbar). Was hier nicht gemacht werden kann, muß mit dem Kern ausgeglichen werden. Dazu müssen wir uns einige typische Blechschnitte und Blechqualitäten ansehen.
.
Die verschiedenen Kern-"Schnitte" bei den Übertragern
Für Übertrager kommen überwiegend M- und Ei-Schnitte in Frage, weniger oft werden SM-Kerne verwendet. Der Ringkern wird für eine Reihe von Spezialanwendungen eingesetzt. Aber M-Kern ist nicht gleich M-Kern, und Ei-Kern ist nicht gleich Ei-Kern, usw.
Hier kommt es auf eine Reihe von Details an, einmal entsteht ein Spitzenübertrager, das andere Mal ist es mehr ein Drahthaufen mit Blechkern. Wickeltechnisch ist der Ringkern am schlechtesten beherrschbar, denn eine saubere Lagenwicklung ist hier unmöglich. Ebenfalls ist eine Vakuumtränkung nur bedingt möglich, da es nicht wie beim normalen Spulenkörper für den Lack Eindringmöglichkeiten in den Wickel gibt. Die Vakuumtränkung ist aber sehr vorteilhaft, da sie Wickel und Kern einmalig und definiert festlegt. Außerdem werden Isolationsfestigkeit und Widerstandsfähigkeit gegen Feuchtigkeit erhöht.
.
Das Wissen um die Eigenschaften von Trafoblechen
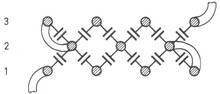
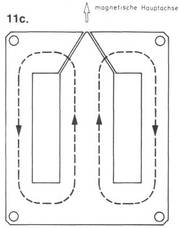
Was wir bis jetzt noch nicht berücksichtigt haben, sind Einzelheiten der Trafobleche. In Bild 11 sind einige gängige Trafobleche, sogenannte Mantelkerne, zusammengestellt, die gut für den Bau von Übertragern geeignet sind. Bevor wir auf die Besonderheiten bei den einzelnen Blechschnitten eingehen, sind erst die prinzipiellen Betrachtungen zu machen.
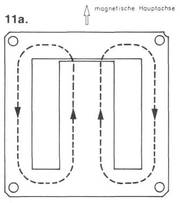
Fangen wir bei Bild 11a an, und untersuchen wir zunächst, was im Kern vorgeht. Die Breite der Zunge bestimmt zusammen mit der Pakethöhe den Eisenquerschnitt. Die Zunge, in der der Hauptfluß der Feldlinien liegt, steckt im Spulenkörper, auf dem die Wicklungen untergebracht sind. Querstege und Schenkel schließen den magnetischen Kreis und sorgen dafür, daß die Feldlinien sich möglichst vollständig darin bewegen.
Bei unserem M-102-Blechschnitt ist die Zunge 34mm breit. Da sich die Feldlinien je zur Hälfte auf linke und rechte Schenkel und Querstege aufteilen, genügt hier die halbe Breite von 17mm.
Leider folgen jedoch die Feldlinien nicht unbedingt freiwillig dem vorgegebenen Weg, da sie, bedingt durch die Wicklungsanordnung, eine Vorzugsrichtung haben (Bild 11a).
Diese Vorzugsrichtung wird außerdem noch an einer Stelle unterbrochen, was sich technisch leider nicht vermeiden läßt, da die Bleche ja irgendwie in den Spulenkörper eingeschoben werden müssen. An dieser Stelle ergibt sich ein kleiner Luftspalt, der den Feldlinien einen ungleich höheren Widerstand entgegenstellt als das Eisenblech. Ein Luftspalt von 0,1 ... 0,2mm ist - bei dieser Blechart bedingt durch den Stanzvorgang - üblich.
.
Der Standard-M-Schnitt
Der Standard-M-Schnitt hat nun prinzipbedingt einige gravierende Nachteile. Der unvermeidbare Luftspalt befindet sich genau an der Stelle, an der die meisten Feldlinien vorhanden sind und zudem noch ihre Richtung um 90 Grad ändern sollen. An solchen Stoßstellen kann nur mit der halben Blechstärke gerechnet werden, was den Magnetisierungsaufwand erhöht.
Streuverluste sind dadurch unvermeidbar. Durch wechselseitige Schichtung kann die Wirkung des Luftspaltes verringert werden, durch einseitige Schichtung wird sie erhöht (dies ist bei bestimmten Anwendungen erwünscht).
Der M-Schnitt wurde und wird für Übertrager verwendet, hat aber aufgrund der Trennfuge an ungünstiger Stelle prinzipbedingt ein höheres Streufeld. Durch erhöhten Schachtelaufwand in der Wicklung muß versucht werden, Kapazität und Streuinduktivität in den Griff zu bekommen, da sonst die Resonanzspitze (siehe Bild 7) zu groß wird und unter Umständen im Übertragungsbereich liegt.
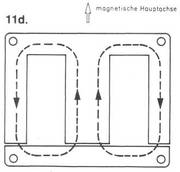
Der PM-Schnitt
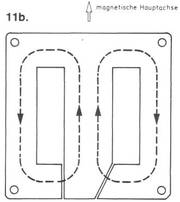
Der zweite gebräuchliche M-Schnitt ist der PM, wie in Bild 11b abgebildet. Eine gerade und eine schräge Trennfuge ermöglichen vierfache Verschachtelung der Bleche, so
daß die Wirkung des Luftspaltes nahezu aufgehoben wird. Die Trennfugen sind außerdem an der Stelle am Blech angeordnet, an der die Feldliniendichte nicht mehr so hoch ist.
Eine weitere Änderung gegenüber dem M-Blech sind die verstärkten Querstege und Schenkel. Der magnetische Kreis hat dadurch einen geringeren Widerstand, es können mehr Feldlinien im Eisen gehalten werden, und die Verluste sinken.
Dadurch wird die Leistungsfähigkeit bei gleichem Eisenquerschnitt erhöht, das Streufeld gleichzeitig erniedrigt. Der Nachteil am PM-Kern ist der erhöhte Schachtelungsaufwand.
Der MD-Schnitt
Als weiteren M-Schnitt gibt es den MD-Kern, wobei hier das D für diagonal steht, was sich auf die Lage der Trennfugen bezieht. In Bild 11c ist dieser Blechschnitt abgebildet. Auffallend sind hier die besonders breiten Querstege, die noch breiter als beim PM-Schniti sind. Die Schenkel sind genauso breit wie beim Standard-M-Schnitt.
Der Sinn dieser Konstruktion ist folgender: Die Trennfugen sind so in dem Bereich der geringsten Feldliniendichte angeordnet, daß der geringe Luftspalt praktisch wirkungslos ist und den Feldlinien kaum Widerstand entgegensetzt.
Dadurch wird dieser Kern sehr streuarm, bei richtiger Montage sogar streuärmer als die Ringkerne !
Bedingt durch die hervorragende Streuarmut lassen sich mit diesem Blechschnitt Übertrager mit geringerem Schachtelaufwand bauen, die von Haus aus eine relativ geringe Streuinduktivität aufweisen.
Der EI-Schnitt
Als letzten Kern betrachten wir noch den Ei-Schnitt (siehe Bild 11). Dieser ist besonders für Übertrager geeignet, die einen Luftspalt benötigen. Eintakt-A-Endstufen liefern nicht nur Wechselstrom, sondern haben am Ausgang einen Gleichstromanteil.
Damit der Eisenkern nicht schon durch den Gleichstromanteil so hoch vormagnetisiert und dann durch den Wechselstrom in die Sättigung getrieben wird, muß er durch einen Luftspalt kompensiert werden. Hier bietet sich der Ei-Schnitt besonders an, da je nach Abstand von I zu E ein definierter Luftspalt eingestellt werden kann.
.
Ist der Artikel Teil 1 hier wirklich zu Ende ? Da stand etwas von Fortsetzung ....
.