Etwas mehr über die echte NF-Leistungsmessung . . .
- 5% sind zum Messen viel zu ungenau
Natürlich kann man an einen Stereo-Endverstärker hinten "irgend- welche" 8Ω Drahtwiderstände anklemmen und mit Oszilloskop und Voltmeter die Spannung messen, bis zu der das Sinus-Signal noch nicht "klippt" (verzerrt) - und dann mit dem Taschenrechner die Leistung ermitteln. Doch das ist mühsam und nichts von Dauer. Außerdem schleichen sich ganz schnell Meß-Fehler ein, die die Laune trüben. Denn merke : "Wer viel mißt, mißt Mist".
Der zweite Ansatzpunkt ist eine vernünftige Meßgenauigkeit
Wie genau benötige ich das Meßergebnis ? Muß es unterhalb des 1% Bereiches zwecks "gerichtsfester" Beweise (Werte) liegen oder möchte ich nur wissen : Macht der Endverstärker auf beiden Kanälen die im Datenblatt spezifizierte Ausgangsleistung über 10 Minuten ? Benötige ich diese Angaben für 4Ω, 8Ω und für 16Ω Messungen oder reicht die 8Ω Messung aus.
Radio RIM hatte 1983 zwei Leistungsmesser im Programm
In den RIM Katalogen um 1983 findet man zwei Leistungs- meßgeräte SWM 3000 und SWM 6000, sogar als Bausätze.
Und im Katalog 1983 gibt es eine Beschreibung, wie die Ausgangs-Leistung korrekt gemessen werden sollte.
.
Echte NF-Leistungsmessung - Unabhängig von der Kurvenform
Viele Verstärker auf dem ELA- und Hifi-Markt besitzen eine integrierte „Leistungsanzeige".
Alle Messungen funktionieren nach dem Prinzip der Spannungsmessung bezogen auf einen „idealen ohmschen Lastwiderstand". Den Anzeigen darf man (aber nur dann) Glauben schenken, wenn Folgendes uneingeschränkt erfüllt ist:
.
Die Bedingungen sind :
.
- 1. Das verstärkte Signal ist rein sinus-förmig!
- 2. Die angeschlossene Last ist „ideal ohmisch"
.
Dann gilt :
Momentanleistung (Peak):
P = U • I = u²/R;
wobei u und i = Momentanwerte sind und R = eine ideale ohmsche Last
Mittelwertsleistung (VU):
P = U • li = U²/R;
wobei U; I = Effektivwerte sind und R = eine ideale ohmsche Last
Da das Quadrieren und die Effektivwertbildung auf elektronischem Weg für diese relativ simple Anwendung zu aufwendig ist, werden die Skalen entsprechend (oft logarithmisch) ausgelegt. Selbstverständlich gilt diese Skala dann nur für saubere Sinus-Frequenzen !
.
Also so geht das in der Praxis nicht !
- ein rein sinusförmiges Signal
- und das hier wollen wir messen
In der Praxis werden die beiden obigen Bedingungen nicht mal im "Entferntesten" erfüllt!
- Musik besteht aus vielen einzelnen Sinusschwin- gungen verschiedener Frequenzen und Amplituden.
- Es gibt keine idealen ohmschen Lasten, schon gar nicht bei Lautsprechern ! Klare Aussagen liefern Impedanz-Diagramme Z = f (f).
Die Lautsprecher- "Impedanz"-Angaben mit 4 Ω oder 8 Ω sagen lediglich aus, daß bei keiner Betriebsfrequenz der Anschlußwert unter 3,2 Ω bzw. 6,4 Ω sinkt! Mehrwege- Lautsprecherboxen erreichen oft ... 100 Ω !
.
Es gibt auch keine "idealen" ohmschen Drahtwiderstände .
- Unsere Meßwiderstände -8 Ohm mit 1% Genauigkeit (aber kalt !) dafür 250 Watt Belastbarkeit für ein paar Minuten
- RADIO RIM Modell SWM 3000
Verstärker-Prüfungen werden gewöhnlich mittels Spannungs- messung an einem hochbelastbaren und hochgenauen ohmschen Drahtwiderstand (mit 1% Genauigkeit) vorgenommen.
Aber auch teure Hochlastwiderstände (Bild rechts), die als L-arm und C-arm (also wirklich rein ohmsche Werte = fast keine Induktivität und fast keine Kapazität) klassifiziert werden, weichen bei Frequenzen über 10 ... 20 kHz stark vom „Ideal" ab.
Der Meß-Widestand wird nach wenigen Minuten erheblich warm (besser gesagt glühend heiß) und dann "läuft" der 1% Widerstandswert "etwas" weg - er wird bei deutlicher Hitze größer und schon stimmen die Messungen nicht mehr.
Frequenzgang- und Klirrfaktormessungen dieser Methode täuschen dann über die wahren Daten (Werte) hinweg !
.
Wie wird die Leistung korrekt berechnet ?
Die mittlere Leistung P berechnet sich unabhängig von Signalverlauf und Art der Last nach :
wobei u und i = Momentanwerte sind. (Das Ganze ist hier recht oberflächlich bzw. allgemein erläutert und müsste noch präzisiert werden).
Schaltungstechnisch müssen also die Momentanwerte von Lastspannung und Laststrom gemessen und miteinander multipliziert werden. Das Resultat wird anschließend periodisch "integriert" (das ist der mathematische Begriff für "pro Zeiteinheit aufsummiert"), und liefert dann dem (analogen) Anzeigeinstrument einen - der tatsächlichen Wirkleistung - proportionalen Meß-Strom (und damit eine korrekte Anzeige). Wegen dieser Proportionalität ist die Skala also linear !
.
Randbedingung : Strom und Spannung können durchaus die entgegengesetzte Polarität haben !!!!
.
Ein Versuch, es besser zu erklären :
.
- ein sauberer Sinus
- ein verzerrter Sinus
- Anmerkung :
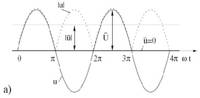
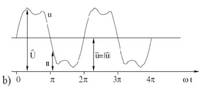
Auf dem Oszilloskop wird die mehr oder weniger sinus- förmige Kurvenform in Form der Hüllkurve angezeigt - und bildlich gesehen - berechne ich diese Flächen der beiden Signalhälften oberhalb und unterhalb der Null-Linie, das sind die von dieser Hüllkurve eingeschlossenen Flächen - mit Hilfe der Integralrechnung.
In meinem Meßgerät benötige ich also einen Integrator- Baustein, das wäre eine elektronische Schaltung, der mir diese aufsummierten Flächen unabhängig von der Signal- form errechnet und ausgibt. Heute macht das ein Taschenmeßgerät für 20 Euro oder der PC in Milli- sekunden, in 1983 war es eine Kunst, soetwas in einem Chip zu automatisieren.
Die Crux an der Sache ist durchaus verständlich zu erklären :
Mit einem Drahtwiderstand, einer sogenannten ohmschen (realen) Last, sind die zu multilizierenden Werte von Spannung und Strom immer positiv. Dagegen mit einem Lautsprecher als (induktiver oder sogar kapazitiver) Last kann es durchaus vorkommen, daß die Spannung positiv ist und zur gleichen Zeit der Strom jedoch negativ ist - oder umgekehrt. Auch diese Werte müssen natürlich multipliziert werden und die ergeben dann ganz andere Werte, nämlich die aktuelle tatsächliche Leistung.
.
Es gab da schon 1976 einen "True RMS" IC von Anlog Devices
- Schon 1976 - alles drinnen
- Der innere Aufbau des Chips
- das Blockdiagramm
Im Datenblatt steht folgendes :
GENERAL DESCRIPTION
Effektivwertmessung = "RMS" Messung
bedeutet "root mean sqaure" measurement
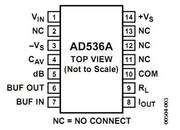
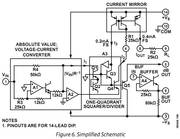
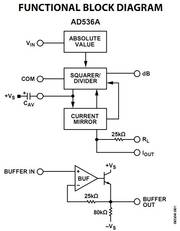
The AD536A (entwickelt 1976) is a complete monolithic integrated circuit that performs "true rms"-to-"dc" conversion. It offers performance comparable or superior to that of hybrid or modular units costing much more. The AD536A directly computes the true rms value of any complex input waveform containing ac and dc components. A crest factor compensation scheme allows measurements with 1% error at crest factors up to 7. The wide bandwidth of the device extends the measurement capability to 300 kHz with less than 3 dB errors for signal levels greater than 100 mV.
An important feature of the AD536A, not previously available in rms converters, is an auxiliary dB output pin. The logarithm of the rms output signal is brought out to a separate pin to allow the dB conversion, with a useful dynamic range of 60 dB. Using an externally supplied reference current, the 0 dB level can be conveniently set to correspond to any input level from 0.1 V to 2 V rms. The AD536A is available in two accuracy grades. The AD536AK offers a maximum total error of ±2mV ±0.2% of reading.
The AD536A computes the true root-mean-square level of a complex ac (or ac plus dc) input signal and provides an equivalent dc output level. The true rms value of a waveform is a more useful quantity than the average rectified value because it relates directly to the power of the signal. The rms value of a statistical signal also relates to its standard deviation.
.
Das bedeutet, der Chip wertet jede Art von Eingangssignal aus, selbst wenn auch noch überlagerte Gleichspannunganteile dabei sind. Das kommt natürlich bei unseren Endstufen nicht vor, es wäre auch gefährlich für die Boxen.
.
Weiterhin erzeugt der Chip ein Signal für eine dB Pegel-Anzeige für ein analoges Zeigerinstrument. Und das alles gab es bereits 1976 !!
.
.
